第十一周学习总结
一、学习目标
了解图的分类
了解图的遍历
常用图算法
图的实现策略
二、学习内容
1.图的分类
① 无向图：
表示边的顶点对是无序的图被称为无向图
无向图中若任意两个顶点间都有一条边的话该图就被称为完全图
② 有向图：
图中的边是顶点的有序对的图称为有向图
有向图中如果任意两个顶点间都有路径相连该图被称为连通图
③ 带权图：
在有向图或无向图中若每条边都对应一个权值则称为带权图
2.图的遍历
① 深度优先：
深度优先遍历也叫深度优先搜索(depth-first traversal)。它的遍历规则：
不断地沿着顶点的深度方向遍历。顶点的深度方向是指它的邻接点方向。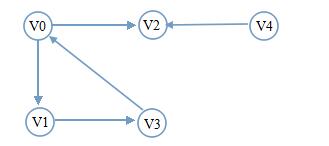
如图：从V0开始遍历 遍历分析：V0有两个邻接点V1和V2，选择下标最小的V1遍历。接着从V1开始深度遍历，V1只有邻接点V3，也就是没有选的：遍历V3。接着从V3开始遍历，V3只有邻接点V0，而V0已经被遍历过。此时出现了上面提到的情况一，开始回溯V1，V1无未被遍历的邻接点，接着回溯V0，V0有一个未被遍历的邻接点V2，新的一轮深度遍历从V2开始。V2无邻接点，且无法回溯。此时出现了情况二，检测visited[i]，只有V4了。深度遍历完成。 ② 广度优先：
广度优先遍历也叫广度优先搜索(breadth-first traversal)。它的遍历规则：
1.先访问完当前顶点的所有邻接点。(应该看得出广度的意思) 2.先访问顶点的邻接点先于后访问顶点的邻接点被访问。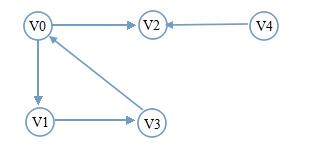
同样的图：从V0开始遍历 遍历分析：V0有两个邻接点V1和V2，于是按序遍历V1、V2。V1先于V2被访问，于是V1的邻接点应先于V2的邻接点被访问，那就是接着访问V3。V2无邻接点，只能看V3的邻接点了，而V0已被访问过了。此时需检测visited[i]，只有V4了。广度遍历完毕。 3.常用图算法
最小生成树
因为树总是图，对于有些图来说，图本身就是一颗生成树，所以这样的图的生成树中将包含全部的边。
最小生成树是其所含边的权值之和小于等于图的任意其他生成树的边的权值之和的生成树。
通常构造最小生成树的算法有两种：
** ① Prim算法：**
它是从点的方面考虑构建一颗MST，大致思想是：设图G顶点集合为U，首先任意选择图G中的一点作为起始点a，将该点加入集合V，再从集合U-V中找到另一点b使得点b到V中任意一点的权值最小，此时将b点也加入集合V；以此类推，现在的集合V={a，b}，再从集合U-V中找到另一点c使得点c到V中任意一点的权值最小，此时将c点加入集合V，直至所有顶点全部被加入V，此时就构建出了一颗MST。因为有N个顶点，所以该MST就有N-1条边，每一次向集合V中加入一个点，就意味着找到一条MST的边。
** ② Kruskal算法：** 假设 WN=(V,{E}) 是一个含有 n 个顶点的连通网，则按照克鲁斯卡尔算法构造最小生成树的过程为：先构造一个只含 n 个顶点，而边集为空的子图，若将该子图中各个顶点看成是各棵树上的根结点，则它是一个含有 n 棵树的一个森林。之后，从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图，也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之。依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。
4.图的实现策略
① 邻接表：
对于图来说，因为每个结点可以通过最多n-1条边与其他结点相连，所以最好使用链表来保存每个结点的边，这个链表就称为邻接表。对于带权图，每条边应该用包含了权值的三元组来保存。对于无向图，边（A,B）在顶点A和顶点B的两个邻接表中都应该出现。
② 邻接矩阵：
用一个一维数组存放图中所有顶点数据；用一个二维数组存放顶点间关系（边或弧）的数据，这个二维数组称为邻接矩阵。用邻接矩阵表示图，很容易确定图中任意两个顶点是否有边相连。邻接矩阵分为有向图邻接矩阵和无向图邻接矩阵。对无向图（无向简单图）而言，邻接矩阵一定是对称的，而且对角线一定为零，有向图则不一定如此。
三.
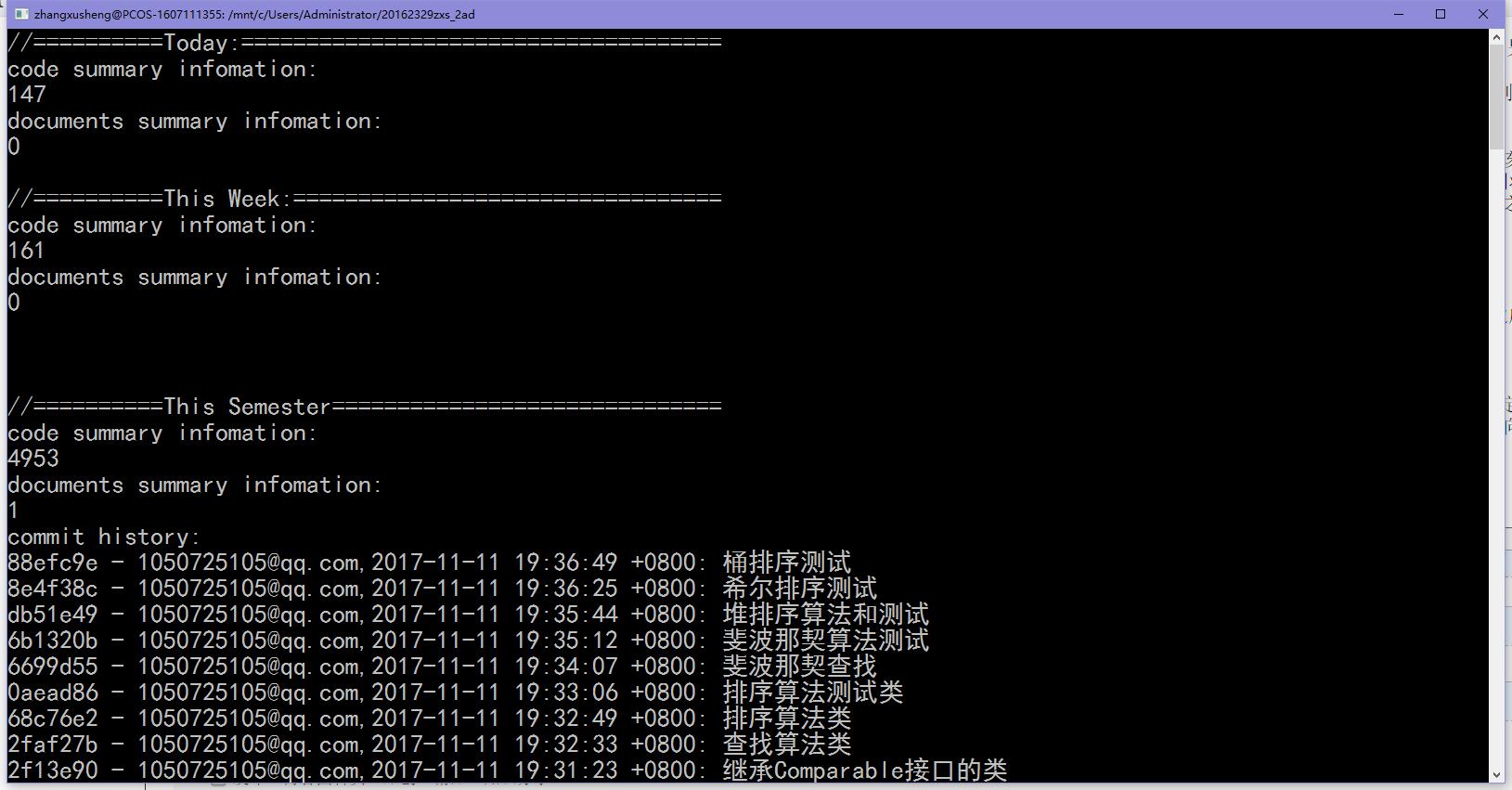
四.点评模板：
- 博客中值得学习的或问题：
- 界面很好看
- 问题分析可以更详细
其他
希望我们结对在这学期能相互促进，技术更上一层楼。本周结对学习情况
- 结对学习内容
- 一起讨论学习。
- 结对学习内容
五.学习进度条
| 代码行数（新增/累积） | 博客量（新增/累积） | 学习时间（新增/累积） | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 0/0 | 1/2 | 10/20 | 了解数据结构及算法 |
| 第二周 | 664/664 | 2/3 | 10/20 | 系统的学习了查找和排序 |
| 第五周 | 1333/1997 | 2/5 | 15/60 | 栈数据结构的学习 |
| 第七周 | 812/3035 | 2/7 | 15/80 | 树的学习和实现 |
| 第九周 | 1364/4399 | 2/9 | 15/110 | 二叉查找树、哈夫曼树、堆 |
| 第十一周 | 554/4953 | 1/10 | 15/140 | 图的理解实现 |